Movimiento
El estudio del movimiento es fundamental en la física, ya que nos permite comprender cómo y por qué se desplazan los objetos en nuestro universo.
Desde la caída libre de una manzana hasta el complejo vuelo de una nave espacial, el movimiento abarca una gama extensa de fenómenos naturales y tecnológicos.
Comprender el movimiento de un objeto nos permite crear un sistema con ecuaciones que determinarán la posición, la velocidad y la aceleración del cuerpo en cada instante de tiempo.
Simulacion de particulas donde su atraccion o repulsion estan en funcion de la distancia entre ellas y su color.
Distancia \( d \)
Representa la cantidad de espacio que hay entre dos puntos.
Matematicamente se expresa como la diferencia entre el punto final y el inicial.
$$ d = x_{f}-x_{i} $$
Esta diferencia tambien se puede representar como un "cambio" con el siguiente simbolo.
$$ \Delta x = x_{f}-x_{i} $$
Dependiendo la situacion podemos utilizar otros simbolos para representar distancia o posicion algunos de los mas comunes son los siguientes:
$$ d$$
$$ \Delta x $$
$$ x_{f}-x_{i} $$
$$ r $$
$$ x $$
$$ y $$
$$ z $$
Cuando la posicion es en mas de una dimension, utilizamos otros simbolos para respresentar la distancia conforme el plano de referencia.
$$ x, y, z $$
$$ x = izquierda-derecha $$
$$ y =arriba-abajo $$
$$ z = adelante-atras $$
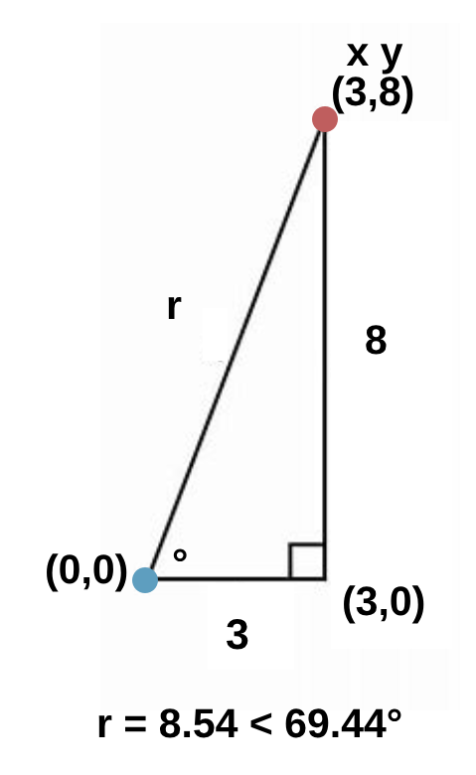
Por ejemplo, en dos dimensiones podemos ubicar un objeto en las cordenadas (x, y)
$$ x = 3 $$
$$ y = 8 $$
3 unidades a la derecha (+x) y 8 unidades hacia arriba (+y).
La figura que se forma entre dos puntos es equivalente a un triangulo.
Al estar en mas de una dimension, la posicion tiene direccion.
Esta posicion se puede representar como un vector.
Un vector tiene magnitud y un angulo de direccion.
En este caso la magnitud es la hipotenusa del triangulo y el angulo representa la inclinacion de la linea.
La hipotenusa del triangulo representa la distancia total desde el origen al punto mencionado.
Para obtener la magnitud de ambos ejes combinados utilizamos el Teorema de Pitagoras, donde la hipotenusa es la distancia (magnitud) desde el origen hasta la coordenada (x,y)
$$ r = \sqrt{\Delta x^2 + \Delta y^2} $$
Para obtener la inclinacion usamos las funciones trigonometricas:
$$\sin(\theta) = \frac{\text{y}}{\text{r}}$$
$$\cos(\theta) = \frac{\text{x}}{\text{r}}$$
$$\tan(\theta) = \frac{\text{y}}{\text{x}}$$
Para obtener el angulo usamos las funciones trigonometricas inversas:
$$ \sin^{-1}(\frac{\text{y}}{\text{r}}) = \theta$$
$$ \cos^{-1}(\frac{\text{x}}{\text{r}}) = \theta$$
$$ \tan^{-1}(\frac{\text{y}}{\text{x}}) = \theta$$
Distancia en dos dimensiones.
Ejemplo para calcular la hipotenusa de un triangulo y su angulo de inclinacion.
Magnitud
Angulo
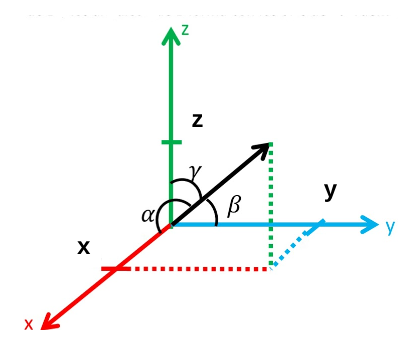
Para tres dimenciones: (x,y,z)
$$ r = \sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2} $$
Distancia en tres dimensiones.
Ejemplo para calcular la magnitud y ángulos correspondientes entre dos puntos en el espacio.
Magnitude
Alpha
Beta
Gamma
Velocidad \( v \)
Representa el cambio de distancia en cierto tiempo.
Matematicamente se expresa como la division o relacion entre estas dos unidades.
$$ v = d/t $$
$$ v = x/t $$
Si se viajo 200 metros en una cantidad de 50 segundos, tenemos una velocidad de (200/50) = 4 metros por segundo.
La velocidad tambien se representa como el "cambio" de estas dos unidades.
$$ v = \Delta x / \Delta t $$
Cuando el incremento entre las magnitudes es infinitesimal se convierte en una derivada
La velocidad es la derivada de la distancia con respecto al tiempo.
$$ v = \frac{dx}{dt} $$
Esto significa que si tenemos una formula o funcion que nos describa la distancia o posicion de un objeto, la derivada de esta funcion, es una nueva funcion que explica la velocidad del objeto.
Title Obj
Subtitle Obj
This is a simple description object, demonstrating a centered paragraph within the Bootstrap framework.
Inline Math: \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
Centered Math: $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$$