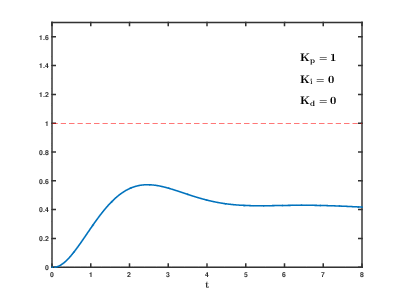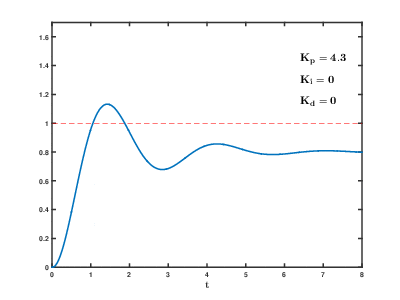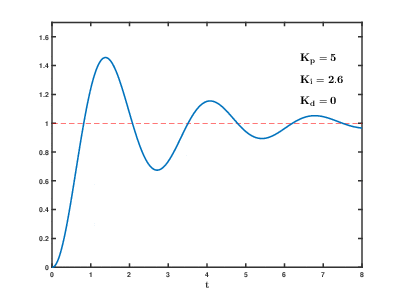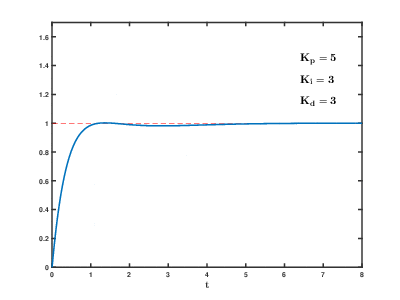
Un controlador PID es un dispositivo que regula una variable de un proceso para que coincida con un valor deseado utilizando un algoritmo que combina tres acciones: proporcional, integral y derivativa.
Estas acciones hacen que el controlador PID sea más suave y eficiente que otros tipos de control.
El control PID se aplica a sistemas que requieran de una alta precisión, en donde la salida final del sistema debe ser lo más cercana a la salida deseada.
Además, con estos controladores se logra ajustar parámetros como la velocidad de respuesta y el sobrepaso, vitales en ciertos sistemas.
El control PID es el controlador más adecuado cuando no se tiene conocimiento pleno del proceso, ya que puede compensar las perturbaciones constantes y las variaciones de carga ya que es un algoritmo autoajustable.

El algoritmo PID consiste en calcular la salida aplicada como la suma de los tres componentes, multiplicados por unos factores llamados ganancias.
Estas ganancias determinan la importancia de cada componente y se deben ajustar según las características del sistema y el objetivo de control.
$$S = K_p e + K_i \int e dt + K_d \frac{de}{dt}$$

En un ordenador, o controlador; se utiliza una version discreta del algoritmo ya que se toman intervalos de tiempo definidos para calcular el error.
Nos enfocaremos en la version discreta del algoritmo para entender su funcionamiento.
Este algoritmo se ejecuta una y otra vez en el controlador cada determinado intervalo de tiempo que llamaremos $$\text{tiempo} = t_i$$
Definiremos el error como la diferencia entre el valor esperado (SP) y la variable de proceso (PV).
$$\text{error actual} = SP - PV$$
Calcularemos la parte Proporcional, Integral y Derivativa por separado y las sumaremos al final.
$$Salida = (P) + (I) + (D)$$
La parte proporcional simplemente mulriplica el error por la ganancia proporcional, ya que esta en proporcion a el y el es componente principal, Si el valor de ganancia es 1, la salida es tan grande como lo es el error.
$$P = K_p * \text{error actual}$$
La parte integral multiplica el error actual por la cantidad de tiempo transcurrido y si tiene un valor previo se le suma, guardando un historial de la magnitud anterior.
$$ I = I+(K_i\times{\text{error actual}}\times{t_i}) $$
La parte derivativa primero calcula la diferencia entre el error anterior (si es que existe) y el error actual, despues se divide entre el tiempo y se multiplica por la ganancia.
$$D = K_d ( \frac{\text{error actual}-\text{error previo}}{t_i})$$
Al sumar estos terminos tenemos nuestra salida
$$Salida = (P) + (I) + (D)$$
Para inicial el ciclo nuevamente tenemos que definir el error anterior como el error actual y volver a empezar el algoritmo
$$\text{error previo} = \text{error actual}$$
El ciclo aqui se repite una y otra vez hasta que el error disminuye y la salida de hace cero, logrando estabilidad, cualquier perturbacion causara un auto regrezo al exigir que el error sea cero.
Concideraremos que nuestra variable tiene 10 unidades de error y la siguiente sintonia: $$\text{error actual} = 10$$
$$t_i = 0.01$$ $$K_p = 1$$ $$K_i = 1$$ $$K_d = 0.01$$
La parte proporcional
$$P = K_p * \text{error actual}$$
$$10 = 1 * 10$$
La parte integral
$$ I = I+(K_i\times{\text{error actual}}\times{t_i}) $$ $$ 0.1 = 0+(1\times{10}\times{0.01}) $$
La parte derivativa
$$D = K_d ( \frac{\text{error actual}-\text{error previo}}{t_i})$$ $$10= 0.01 ( \frac{\text{10}-\text{0}}{0.01})$$
Al sumar estos terminos tenemos nuestra salida
$$Salida = (P) + (I) + (D)$$ $$20.1 = (10) + (0.1) + (10)$$
Para iniciar el ciclo nuevamente tenemos que definir el error anterior (actual mente 0) como el error actual y volver a empezar el algoritmo
$$\text{error previo} = \text{error actual}$$ $$\text{error previo} = \text{10}$$
Repetiremos el ciclo una vez mas suponiendo que la variable cambio 3 unidades y el error disminuyo a 7
$$\text{error actual} = 7$$
La parte proporcional
$$P = K_p * \text{error actual}$$
$$7 = 1 * 7$$
La parte integral
$$ I = I+(K_i\times{\text{error actual}}\times{t_i}) $$ $$ 0.17 = 0.1+(1\times{7}\times{0.01}) $$
Note como la parte anterior del error inegral 0.1 se acumulo en este paso.
La parte derivativa
$$D = K_d ( \frac{\text{error actual}-\text{error previo}}{t_i})$$ $$-3= 0.01 ( \frac{\text{7}-\text{10}}{0.01})$$
Note como la parte derivativa se opuso al cambio con un numero negativo en base al error anterior, contrarestando una llegada bursca.
Al sumar estos terminos tenemos nuestra nueva salida
$$Salida = (P) + (I) + (D)$$ $$4.17 = (7) + (0.17) + (-3)$$
Para iniciar el ciclo nuevamente tenemos que definir el error anterior como el error actual y volver a empezar el algoritmo
$$\text{error previo} = \text{error actual}$$ $$\text{error previo} = \text{7}$$
Repetiremos el ciclo una vez mas suponiendo que la variable de proceso se acerco mucho al valor esperado haciendo el error de solo 1 unidad.
$$\text{error actual} = 1$$
La parte proporcional
$$P = K_p * \text{error actual}$$
$$1 = 1 * 1$$
La parte integral
$$ I = I+(K_i\times{\text{error actual}}\times{t_i}) $$ $$ 0.18 = 0.17+(1\times{1}\times{0.01}) $$
Note como la parte integral no alcanzo a tomar grandes valores ya que el ajuste fue muy rapido y no alcanzo a acumular tanto error en el pequeño intervalo de tiempo.
La parte derivativa
$$D = K_d ( \frac{\text{error actual}-\text{error previo}}{t_i})$$ $$-6= 0.01 ( \frac{\text{1}-\text{7}}{0.01})$$
La parte derivativa vuelve a oponerse al notar un cambio en el error anticipando nuevamente la llegada.
Al sumar estos terminos tenemos nuestra nueva salida
$$Salida = (P) + (I) + (D)$$ $$-4.82 = (1) + (0.18) + (-6)$$
Note como ahora la salida se volvio negativa por la parte integral que se opone o acelera el cambio. $$\text{error previo} = \text{error actual}$$ $$\text{error previo} = \text{1}$$
Aqui es donde el error puede hacerse negativo lo cual resultaria en una proporcional negativa tambien y donde poco a poco los valores intengrales tambien lo harian, la derivativa al volverse el error negativo o aproximarse a el se volveria contraria estabilizando aun mas el error. Logrando una leve oscilacion o un punto estable de la variable medida.
Este analisis a pesar de ser corto nos muestra la relacion entre las partes del controlador, se invita a realizar su propio analisis mas detallado para concer mejor las propiedades de este control.
Esta parte es la que mas influencia tiene en el controlador debido a que solo le interesa el error en el momento exacto y es directamente proporcional a el ya sea positivo o negativo.
Esta parte gradualmente va acumulando el error siempre que este persista y lo hace mas despacio que la proporcional.
Esta parte del controlador al aumentar el error rapidamente aumenta su salida, al disminuir el error se opone al cambio contrarestando el efecto de las otras partes incluso aveces volviendose negativa con error positivo anticipando la llegada al punto estable, al no haber un cambio en el error esta parte no hace nada.
import numpy as np
import matplotlib.pyplot as plt
# Definimos los parámetros del PID
Kp = 1 # Ganancia proporcional
Ki = 2 # Ganancia integral
Kd = 0.001 # Ganancia derivativa
Ts = 0.01 # Tiempo de muestreo
N = 1000 # Número de iteraciones
SP = 100 # Valor deseado inicial
# Inicializamos las variables
e = 0 # Error
u = 0 # Acción de control
y = 0 # Salida del proceso
P = 0 # Componente proporcional
I = 0 # Componente integral
D = 0 # Componente derivativo
e_ant = 0 # Error anterior
y_ant = 0 # Salida anterior
# Creamos listas para guardar los resultados
e_list = [] # Lista de errores
u_list = [] # Lista de acciones de control
y_list = [] # Lista de salidas
t_list = [] # Lista de tiempos
# Simulamos el PID
for i in range(N):
e = SP - y
P = Kp * e
I = I + (Ki * Ts * e)
D = Kd * (e - e_ant) / Ts
u = P + I + D
e_ant = e
# Usamos una función de transferencia de primer orden para simular la variable de proceso
# y = (0.85 * u + 0.15 * y_ant) / (1 + 0.15)
# Usamos numpy para simplificar la operación
y = np.divide(np.add(np.multiply(0.85, u), np.multiply(0.15, y_ant)), np.add(1, 0.15))
y_ant = y
e_list.append(e)
u_list.append(u)
y_list.append(y)
t_list.append(i)
# Creamos una figura
plt.figure()
# Graficamos la salida y el valor deseado
plt.plot(t_list, y_list, label="Salida")
plt.plot(t_list, [SP] * N, label="Valor deseado")
# Añadimos etiquetas y título
plt.xlabel("Tiempo (s)")
plt.ylabel("PID (PV)")
plt.title("Ejemplo de PID usando numpy")
# Añadimos una leyenda
plt.legend()
# Mostramos la figura
plt.show()